My research
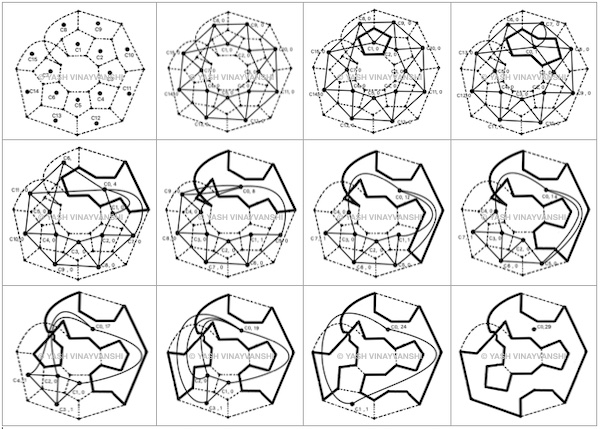
"A new polynomial time heuristic for hamiltonian cycle problem using atomic cycle merging"
The algorithm first discovers all atomic cycles in a graph, then preprocesses the graph using this data to build an intermediate representation called cycle adjacency graph. This CAG maintains information to avoid local decisions leading to unreachability of a vertex and also to guide choice of merging cycles to obtain a larger cycles such that subsequently a hamiltonian cycle is obtained if it exists. This is similar to how a crystal forms, on a seed, the lattice expands.
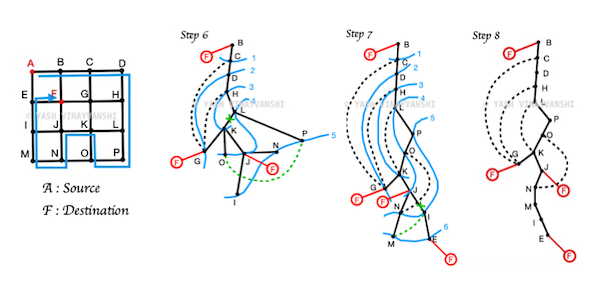
"An Augmented breadth first search for the longest path problem"
The conventional Breadth First search classifies the edges of an undirected graph into tree edges and cross edges. The cross edges can be utilised to prune and implant branches to BFS tree at specific places to find longer paths from source to destination. Other operations such as rotation can also be performed to increase the height of the tree. This indirectly simulates the apical domination in real trees where the shoot tip inhibits growth of axillary buds to increase height of tree instead of breadth. The BFS search space doesnt include the dest. while building the BFS tree, but at the end it attaches dest. to all its neighbours as leaves...
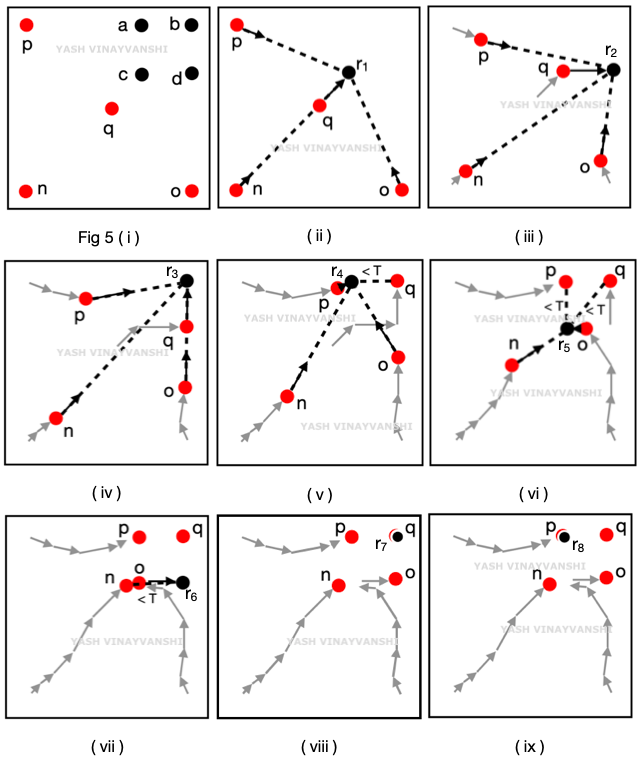
"A new policy for the k-server problem and its analysis"
We present a new deterministic policy for the k-server problem in the general metric space and its competitive analysis. The policy mobilises all servers towards a request by a function of the inverse proportion of their distance from the request. This policy balances the presence of servers in the space so that worst case possibilities exploited by the adversary are reduced and a better competitiveness can be achieved.
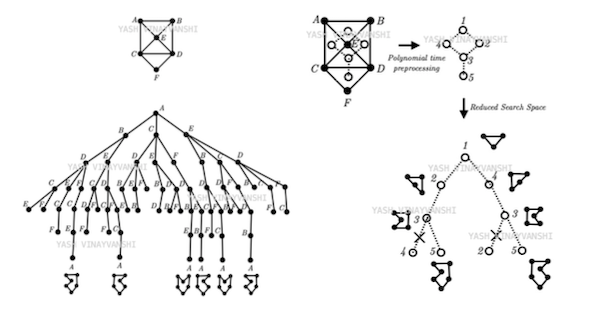
"The art of designing search spaces"
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Quod nam molestiae doloremque possimus, aspernatur sequi distinctio itaque quos unde consectetur! Sed, sapiente accusantium. Natus consectetur dolores voluptate voluptatum modi quaerat accusamus itaque, a vero veritatis, dignissimos magni. Veritatis, sunt. Explicabo pariatur natus in dolorem eius tempora beatae ut, vel fugit modi commodi ad doloremque excepturi libero saepe cupiditate consectetur iure dolores adipisci amet debitis optio nemo! Natus, magnam modi totam incidunt officia nobis molestiae eligendi nam in delectus ipsam doloremque.
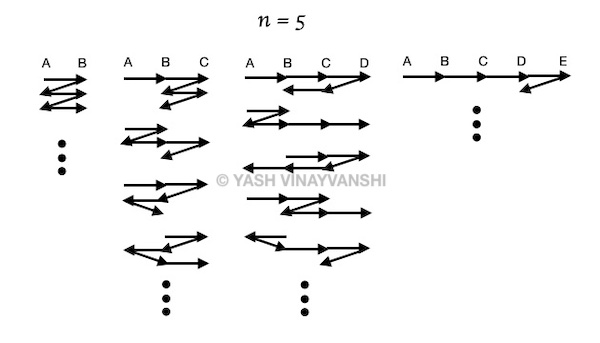
"An attempt to find a mathematical relationship between number of simple paths and number of non simple paths in undirected graphs."
Warshall's algorithm finds the total number of paths of length k between every pair of vertices i, j. However this total count includes simple as well as non simple paths. In problems like finding longest path between two vertices or finding a hamiltonian path, we are intereseted in simple paths. It has been observed that for some graphs, there is a relationship between number of simple paths of length k-1 and number of non simple paths of length k. This fact can be utilised to solve the longest path problem.
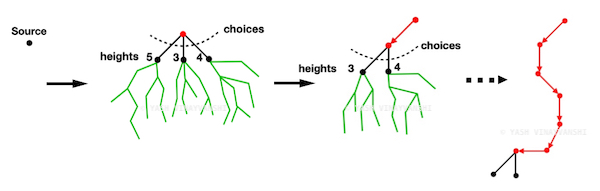
"A new heuristic for hamiltonian path problem using BFS directed DFS."
The problem with combinatorial problems is that the search space is highly non deterministic. For NPC problems, there is no inherent mathematical structure yet found, which can be exploited to build an exact polynomial time solution. The next choice then is to solve by search which if done via brute force is obviously exponenetial in time. Therefore, we try to perform the search intelligently such that we avoid exploring unfruitful parts of search space and devise some guiding mechanism to draw the search toward choices leading to a path to glabal optimal. While taking local decisions, its important to have some kind of global perpective as well to predict the consequences of local choice...
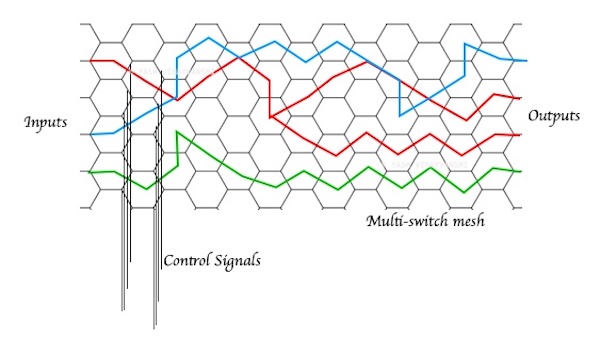
"A path based computing model"
Lorem ipsum dolor sit amet consectetur adipisicing elit. Eaque deserunt, quod minus eveniet cupiditate voluptate laudantium libero hic officia facere quibusdam eos eligendi magni architecto error perferendis tempore incidunt. Saepe dolore tempora inventore quo, totam unde, laudantium necessitatibus doloribus, ducimus tempore explicabo consectetur aliquid harum perspiciatis consequuntur. Nihil, molestias magnam?
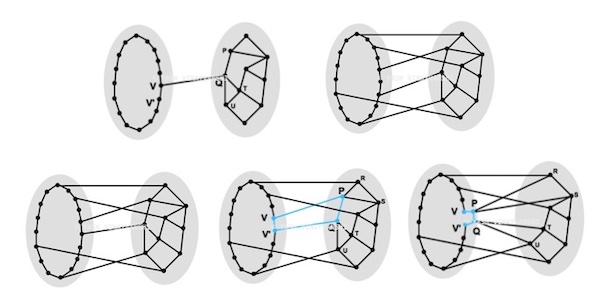
"An augmented Dijkstra's Algorithm as heuristic for the travelling salesman problem."
Lorem ipsum dolor sit amet consectetur adipisicing elit. Officiis vel debitis, reiciendis impedit perferendis cupiditate ea. Omnis esse quo veritatis nesciunt! Quia deleniti sunt nemo molestiae aut optio magni. Possimus amet eius impedit voluptate maiores autem, tempora ducimus esse itaque accusantium placeat molestias animi ipsum, porro quo perferendis iure minus.
"Sorting by Diffusion"
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ipsam odio commodi quas magnam non expedita reiciendis aliquam sint nisi? Modi, laboriosam voluptatum tempora explicabo ipsam veniam voluptatibus maiores dolorum eos similique reiciendis voluptatem ratione unde officia consequatur molestiae vero aperiam iste deleniti, ea omnis natus quo nisi. Reiciendis, corporis aliquid!
Contact Me
yash.vinayvanshi1@gmail.com
©2022 YASH VINAYVANSHI
